
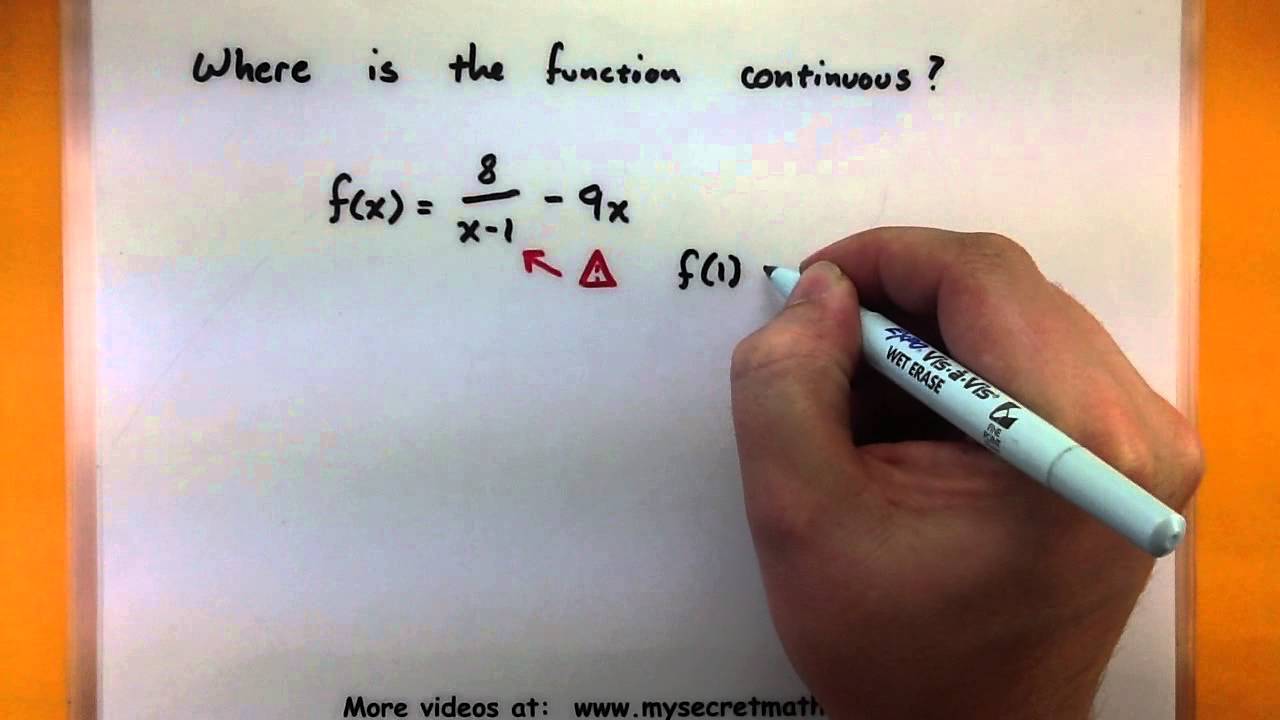
⭐ “Continuity in Functions: A Smooth Ride Through Math”. “How Do You Determine Continuity of a Function?”. Many of the References and Additional Reading websites and Videos will assist you with understating and applying continuity and continuous functions.Īs some professors say: “ It is intuitively obvious to even the most casual observer.“ References See Theoretical Knowledge Vs Practical Application.
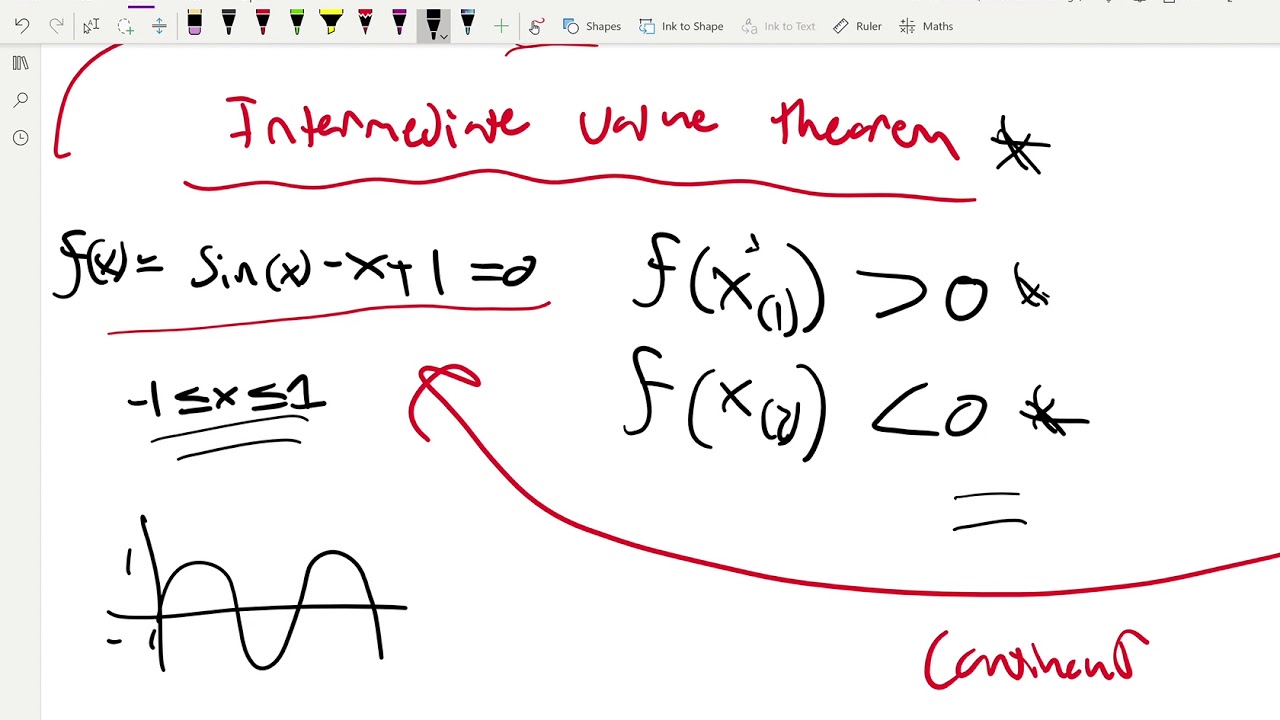
Without continuity, these concepts would not make sense and many problems in mathematics would be unsolvable. Similarly, the integral of a function relies on the continuity of the function. Continuity is one the major requirements of derivability, which is essential for understanding rates of change and the behavior of functions. Whyīut why is continuity so important? Well, in mathematics, continuity is the key to understanding many concepts, including differentiation and integration. But if the question “How close?” is asked, difficulties arise.

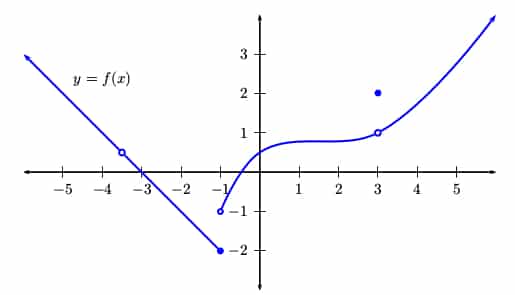
Continuity of a function is sometimes expressed by saying that if the x-values are close together, then the y-values of the function will also be close. A function is a relationship in which every value of an independent variable-say x-is associated with a value of a dependent variable-say y. WhatĬ ontinuity is a rigorous formulation of the intuitive concept of a function that varies with no abrupt breaks or jumps. Without continuity, these models would not accurately represent the behavior of consumers and could lead to flawed predictions about market trends. Utility functions and demand curves are often assumed to be continuous, allowing for smooth transitions between different levels of consumption or demand. In economics, continuity is essential for understanding consumer behavior and market demand. This would not be possible if, as an example, V = V initial + a*t was not continuous! These functions allow us to model the behavior of objects over time and make predictions about their future movements. WhoĬontinuity also has important real-world applications in fields such as physics and economics. For example, the motion of objects can be described using continuous functions, such as position, velocity, and acceleration. When f(x) is continuous for all x in an interval, we say that it is continuous on the interval. Functions that are not defined for all x-values on an interval are also not continuous on that interval. By contrast, there are graphs where the y-value of a given x-value is some distance away from the y-value of an adjacent x-value. When a graph is continuous, it means that you can draw it without lifting your pencil. When you talk about continuity, you describe whether the graph of a function exists for all values of x in an interval, and that these points are adjacent to each other, meaning there are no gaps between any of them. For a = x 1, only the right-hand limit need be considered, and for a = x 2, only the left-hand limit needs to be considered. However, note that at the end-points of the interval I, we need not consider both the right-hand and the left-hand limits for the calculation of lim x→a f(x). The function f(x) is said to be continuous in the interval I = if the three conditions mentioned above are satisfied for every point in the interval I. lim x→a f(x) exists (i.e., the right-hand limit = left-hand limit, and both are finite,.f(a) exists (i.e., the value of f(a) is finite).
Ī function f(x) is said to be continuous at a point x = a, in its domain if the following three conditions are satisfied: Studying about the continuity of a function is really important in calculus as a function cannot be differentiable unless it is continuous. i.e., if we are able to draw the curve (graph) of a function without even lifting the pencil, then we say that the function is continuous. A continuous function, as its name suggests, is a function whose graph is continuous without any breaks or jumps.


 0 kommentar(er)
0 kommentar(er)
